已知函数.(1)求的单调区间;(2)若对于任意的,
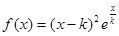 .
.(1)求
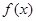 的单调区间;
的单调区间;(2)若对于任意的
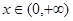 ,有
,有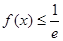 恒成立,求
恒成立,求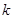 的取值范围.
的取值范围.
(1)求函数的定义域;(6分)(2)求函数在上的值
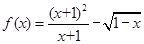 的定义域;(6分)
的定义域;(6分)(2)求函数
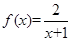 在
在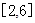 上的值域.(6分)
上的值域.(6分)
函数的递减区间是A.或B.C.或
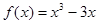 的递减区间是
的递减区间是A.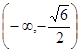 或 或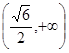
|
B.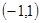
|
C.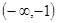 或 或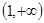
|
D.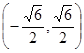
|
函数在[0,2]上的最大值是7,则指数函数在[0,
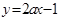 在[0,2]上的最大值是7,则指数函数
在[0,2]上的最大值是7,则指数函数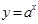 在[0,2]上的最大值与最小值的和为
在[0,2]上的最大值与最小值的和为| A.6 | B.5 | C.3 | D.4 |
已知函数在区间内恒有,则函数的单调递减区间是
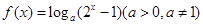 在区间
在区间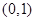 内恒有
内恒有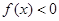 ,则函数
,则函数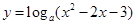 的单调递减区间是 .
的单调递减区间是 .
设函数,且.(1)求的值;(2)若令,求取值范围;
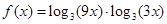 ,且
,且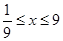 .
.(1)求
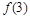 的值;
的值;(2)若令
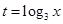 ,求
,求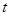 取值范围;
取值范围;(3)将
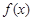 表示成以
表示成以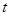 (
(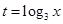 )为自变量的函数,并由此,求函数
)为自变量的函数,并由此,求函数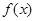 的最大值与最小值及与之对应的x的值.
的最大值与最小值及与之对应的x的值.
已知函数①当时,求函数在上的最大值和最小值;②讨论
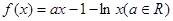
①当
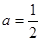 时,求函数在
时,求函数在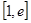 上的最大值和最小值;
上的最大值和最小值;②讨论函数的单调性;
③若函数
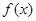 在
在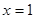 处取得极值,不等式
处取得极值,不等式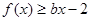 对
对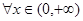 恒成立,求实数
恒成立,求实数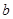 的取值范围。
的取值范围。
下列函数中x=0是极值点的函数是( ) A.
A.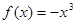
|
B.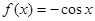
|
C.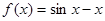
|
D.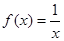
|
已知函数,若在区间上单调递减,则实数的取值范围是(
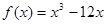 ,若
,若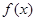 在区间
在区间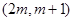 上单调递减,则实数
上单调递减,则实数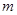 的取值范围是( )
的取值范围是( )A.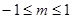
|
B.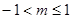
|
C.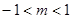
|
D.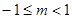
|
函数在上是单调递增函数,则的取值范围是______
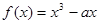 在
在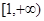 上是单调递增函数,则
上是单调递增函数,则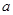 的取值范围是_____________。
的取值范围是_____________。
设函数。(1)求在点处的切线方程;(2)求在区间的
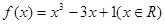 。
。(1)求
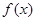 在点
在点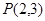 处的切线方程;
处的切线方程;(2)求
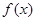 在区间
在区间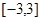 的最大值与最小值。
的最大值与最小值。
已知函数,。(1)求函数的单调区间;(2)若与的图
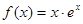 ,
,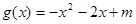 。
。(1)求函数
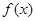 的单调区间;
的单调区间;(2)若
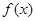 与
与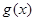 的图象恰有两个交点,求实数
的图象恰有两个交点,求实数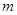 的取值范围。
的取值范围。
已知函数。(1)时,求的最小值;(2)若且在上是单
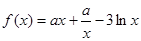 。
。(1)
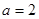 时,求
时,求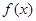 的最小值;
的最小值;(2)若
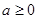 且
且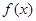 在
在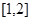 上是单调函数,求实数
上是单调函数,求实数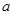 的取值范围。
的取值范围。
定义在上的奇函数满足,且在上单调递增,则A.
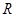 上的奇函数
上的奇函数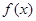 满足
满足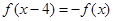 ,且在
,且在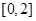 上单调递增,则
上单调递增,则A.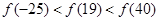
|
B.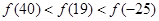
|
C.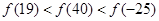
|
D.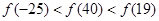
|
已知函数.(1)写出该函数的单调区间;(2)若函数
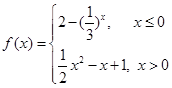 .
.(1)写出该函数的单调区间;
(2)若函数
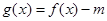 恰有3个不同零点,求实数
恰有3个不同零点,求实数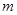 的取值范围;
的取值范围;(3)若
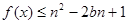 对所有
对所有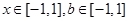 恒成立,求实数n的取值范围。
恒成立,求实数n的取值范围。
已知关于x的函数y=(2-ax)在[0,1]上是减
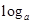 (2-ax)在[0,1]上是减函数,则a的取值范围是
(2-ax)在[0,1]上是减函数,则a的取值范围是| A.(0,1) | B.(1,2) | C.(0,2) | D.[2,+∞)] |
已知,函数(1)求的极小值;(2)若在上为单调增函
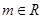 ,函数
,函数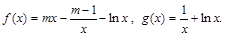
(1)求
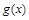 的极小值;
的极小值;(2)若
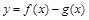 在
在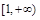 上为单调增函数,求
上为单调增函数,求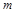 的取值范围;
的取值范围;(3)设
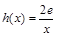 ,若在
,若在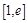 (
(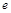 是自然对数的底数)上至少存在一个
是自然对数的底数)上至少存在一个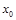 ,使得
,使得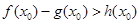 成立,求
成立,求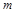 的取值范围.
的取值范围.
设分别是定义在R上的奇函数和偶函数,当时,,且,则
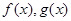 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当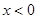 时,
时,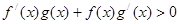 ,且
,且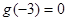 ,则
,则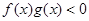 的解集是( )
的解集是( ) | A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D. (-∞,-3)∪(0,3) |
函数的单调增区间与值域相同,则实数的取值为(
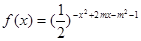 的单调增区间与值域相同,则实数
的单调增区间与值域相同,则实数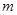 的取
的取值为( )
A.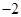
|
B.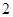
|
C.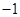
|
D.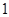
|
已知函数为奇函数,且在处取得极大值2.(Ⅰ)求的解
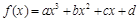 为奇函数,且在
为奇函数,且在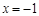 处取得极大值2.
处取得极大值2.(Ⅰ)求
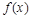 的解析式;
的解析式;(Ⅱ)过点
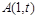 (
(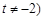 可作函数
可作函数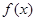 图像的三条切线,求实数
图像的三条切线,求实数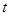 的取值范围;
的取值范围;(Ⅲ)若
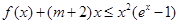 对于任意的
对于任意的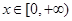 恒成立,求实数
恒成立,求实数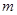 的取值范围.
的取值范围.
下列函数中既是偶函数,又是区间上的减函数的是(
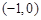 上的减函数的是( )
上的减函数的是( )A.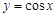
|
B.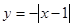
|
C.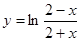
|
D.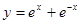
|
已知函数,则=( )A.B.C.
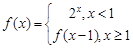 ,则
,则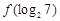 =( )
=( )A.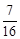
|
B.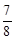
|
C.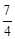
|
D.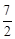
|
(1)已知,求证:;(2)已知,>0(i=1
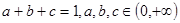 ,求证:
,求证: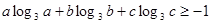 ;
;(2)已知
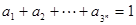 ,
,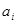 >0(i=1,2,3,…,3n),求证:
>0(i=1,2,3,…,3n),求证: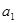
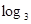
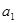 +
+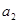
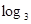
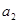 +
+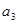
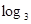
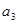 +…+
+…+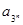
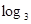
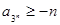
已知函数.(1)若时,取得极值,求实数的值;
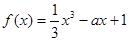 .
.(1)若
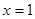 时,
时,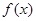 取得极值,求实数
取得极值,求实数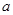 的值;
的值;


(2)求
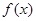 在
在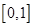 上的最小值;
上的最小值;(3)若对任意
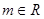 ,直线
,直线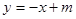 都不是曲线
都不是曲线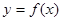 的切线,求实数
的切线,求实数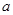 的取值范围.
的取值范围.
若2a+1<3-2a,则实数a的取值范围是(
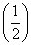 2a+1<
2a+1<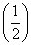 3-2a,则实数a的取值范围是( ).
3-2a,则实数a的取值范围是( ).| A.(1,+∞) | B.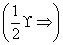
|
| C.(-∞,1) | D.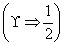
|
已知,,是否存在实数,使同时满足下列两个条件:(1
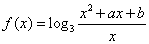 ,
,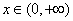 ,是否存在实数
,是否存在实数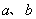 ,使
,使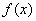 同时满足下列两个条件:(1)
同时满足下列两个条件:(1)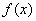 在
在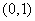 上是减函数,在
上是减函数,在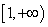 上是增函数;(2)
上是增函数;(2)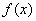 的最小值是
的最小值是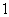 ,若存在,求出
,若存在,求出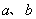 ,若不存在,说明理由.
,若不存在,说明理由.
已知.(1)时,求的极值;(2)当时,讨论的单调性
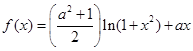
 .
.(1)
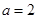 时,求
时,求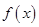 的极值;
的极值;(2)当
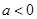 时,讨论
时,讨论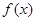 的单调性;
的单调性;(3)证明:
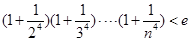 (
(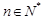 ,
,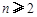 ,其中无理数
,其中无理数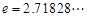 )
)
