题目
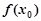 是函数
是函数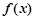 在点
在点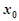 附近的某个局部范围内的最大(小)值,则称
附近的某个局部范围内的最大(小)值,则称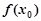 是函数
是函数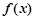 的一个极值,
的一个极值,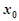 为极值点.已知
为极值点.已知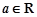 ,函数
,函数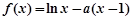 .
.(Ⅰ)若
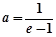 ,求函数
,求函数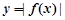 的极值点;
的极值点;(Ⅱ)若不等式
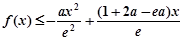 恒成立,求
恒成立,求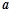 的取值范围.
的取值范围.(
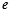 为自然对数的底数)
为自然对数的底数)
答案
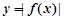 的极小值点为1和
的极小值点为1和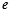 ,极大值点为
,极大值点为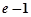 .
.(2)
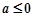
解析
试题分析:解:(Ⅰ)若
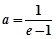 ,则
,则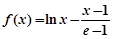 ,
,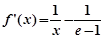 .
.当
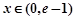 时,
时,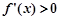 ,
,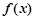 单调递增;
单调递增;当
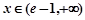 时,
时,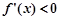 ,
,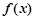 单调递减. …2分
单调递减. …2分又因为
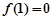 ,
,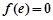 ,所以
,所以当
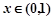 时,
时,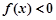 ;当
;当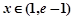 时,
时,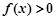 ;
;当
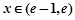 时,
时,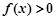 ;当
;当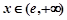 时,
时,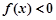 . …4分
. …4分故
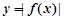 的极小值点为1和
的极小值点为1和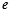 ,极大值点为
,极大值点为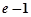 .…6分
.…6分(Ⅱ)不等式
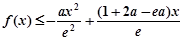 ,
,整理为
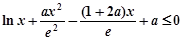 .…(*)
.…(*)设
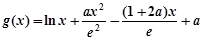 ,
,则
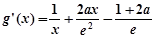 (
(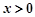 )
)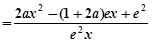
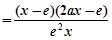 . …8分
. …8分①当
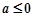 时,
时,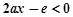 ,又
,又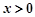 ,所以,
,所以,当
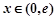 时,
时,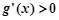 ,
,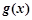 递增;
递增;当
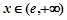 时,
时,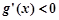 ,
,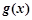 递减.
递减.从而
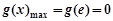 .
.故,
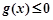 恒成立. …11分
恒成立. …11分②当
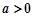 时,
时,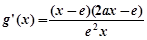
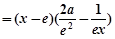 .
.令
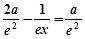 ,解得
,解得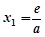 ,则当
,则当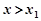 时,
时,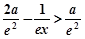 ;
;再令
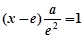 ,解得
,解得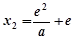 ,则当
,则当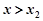 时,
时,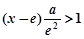 .
.取
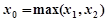 ,则当
,则当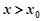 时,
时,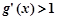 .
.所以,当
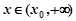 时,
时,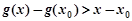 ,即
,即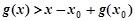 .
.这与“
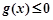 恒成立”矛盾.
恒成立”矛盾.综上所述,
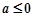 .…14分
.…14分点评:解决的关键是对于导数在研究函数中的运用,求解极值和最值,以及不等式的恒成立问题,属于基础题。
