题目
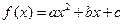 (
(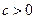 )的导函数的图象如图所示:
)的导函数的图象如图所示:(Ⅰ)求函数
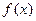 的解析式;
的解析式;(Ⅱ)令
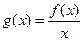 ,求
,求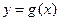 在
在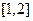 上的最大值.
上的最大值.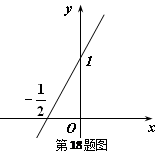
答案
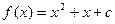 .
.(Ⅱ)当
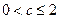 时,
时,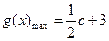 ;当
;当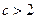 时,
时,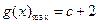 .
. 法二:
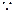 当
当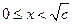 时,
时,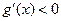 ;当
;当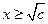 时,
时,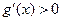 ;
;∴当
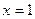 或
或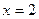 时,
时,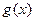 取得最大值,其中
取得最大值,其中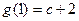 ,
,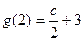 ,
,当
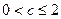 时,
时,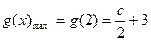 ;当
;当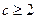 时,
时,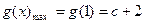 .
.
解析
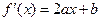 ,由图可知,
,由图可知,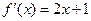 ,
, ∴
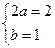 ,得
,得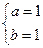 ,故所求函数解析式为
,故所求函数解析式为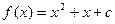 .
.(Ⅱ)
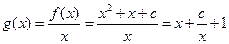 ,
,则
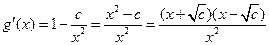 .
.法一:①若
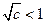 ,即
,即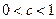 时,
时,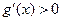 ,
,∴
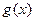 在
在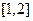 上是增函数,故
上是增函数,故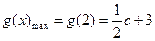 .
. ②若
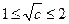 ,即
,即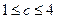 ,当
,当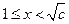 时,
时,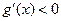 ;当
;当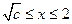 时,
时,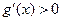 ;
;∵
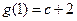 ,
,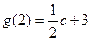 ,
,∴当
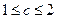 时,
时,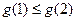 ,
,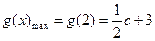 ;
;当
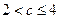 时,
时,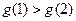 ,
,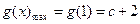 .
. ③若
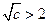 ,即
,即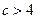 时,
时,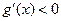 ,
,∴
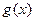 在
在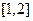 上是减函数,故
上是减函数,故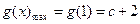 .
. 综上所述,当
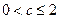 时,
时,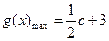 ;当
;当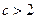 时,
时,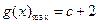 .
. 法二:
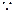 当
当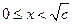 时,
时,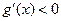 ;当
;当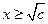 时,
时,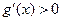 ;
;∴当
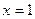 或
或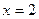 时,
时,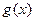 取得最大值,其中
取得最大值,其中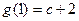 ,
,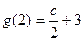 ,
,当
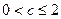 时,
时,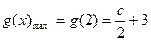 ;当
;当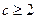 时,
时,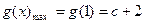 .
.
