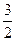题目
已知函数
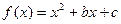 ,对于任意的
,对于任意的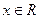 ,恒有
,恒有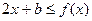 .
.(1)证明:当
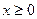 时,
时,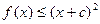 ;
;(2)如果不等式
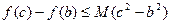 恒成立,求
恒成立,求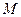 的最小值.
的最小值.
答案
(2)
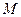 的最小值是
的最小值是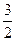
解析
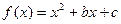 ,对于任意的
,对于任意的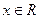 ,恒有
,恒有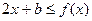
即对于任意的
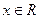 ,
,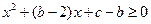 恒成立
恒成立所以
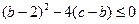 从而
从而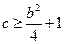
于是
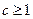 ,且
,且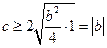 ,
,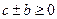
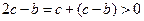
所以,当
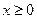 时,
时,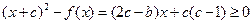
即
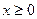 时,
时,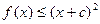
(2)因为
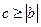 ,所以
,所以当
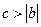 时,由
时,由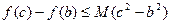 得
得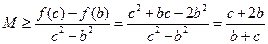 =
=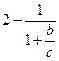
令
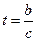 ,因为
,因为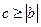 ,所以
,所以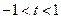
而函数
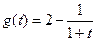 在区间
在区间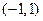 是增函数,所以
是增函数,所以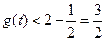
这样,当
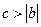 时,
时,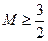
当
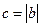 时,由
时,由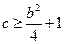 可得
可得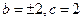 ,
,这时
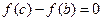 或
或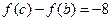 ,
,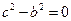
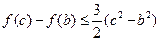 恒成立
恒成立综上所述,
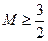 ,
,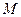 的最小值是
的最小值是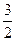
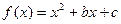 ,对于任意的
,对于任意的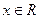 ,恒有
,恒有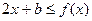 .
.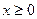 时,
时,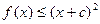 ;
;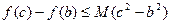 恒成立,求
恒成立,求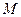 的最小值.
的最小值.
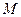 的最小值是
的最小值是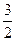
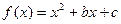 ,对于任意的
,对于任意的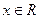 ,恒有
,恒有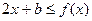
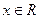 ,
,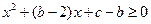 恒成立
恒成立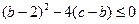 从而
从而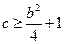
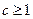 ,且
,且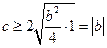 ,
,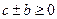
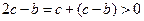
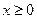 时,
时,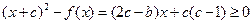
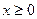 时,
时,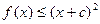
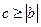 ,所以
,所以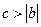 时,由
时,由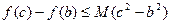 得
得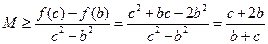 =
=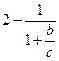
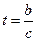 ,因为
,因为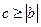 ,所以
,所以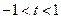
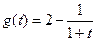 在区间
在区间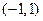 是增函数,所以
是增函数,所以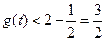
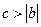 时,
时,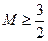
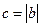 时,由
时,由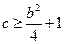 可得
可得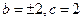 ,
,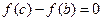 或
或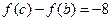 ,
,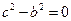
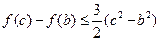 恒成立
恒成立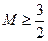 ,
,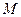 的最小值是
的最小值是