题目
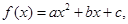 满足
满足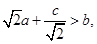 且
且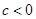 ,则含有
,则含有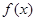 零点的一个区间是( )
零点的一个区间是( )| A.(-2,0) | B.(-1,0) | C.(0,1) | D.(0,2) |
答案
解析
专题:计算题.
分析:根据
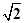 a+
a+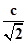 >b,变形为2a+
>b,变形为2a+ 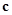 -
-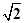 b>0,即2a+
b>0,即2a+ 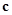 -
-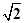 b =f(-
b =f(-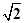 )>0,而f(0)=c<0,从而得到含有f(x)零点的一个区间.
)>0,而f(0)=c<0,从而得到含有f(x)零点的一个区间.解答:解:∵f(x)=ax2+bx+c,且2a+
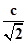 >b且c<0,
>b且c<0,∴f(0)=c<0,
f(-2)=4a-2b+c=2(2a+
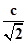 -b)>0,
-b)>0,∴含有f(x)零点的一个区间是(-
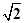 ,0).
,0).故选A.
点评:此题是基础题.考查函数零点的判定定理和不等式的基本性质等基础知识,由2a+
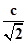 >b得出f(-
>b得出f(-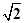 )>0是解题的关键,同时考查了学生灵活应用知识分析解决问题的能力和计算能力.
)>0是解题的关键,同时考查了学生灵活应用知识分析解决问题的能力和计算能力.
