题目
已知函数
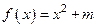 ,其中
,其中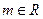 .定义数列
.定义数列 如下:
如下: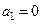 ,
,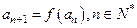 .
.(I)当
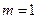 时,求
时,求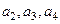 的值;
的值;(II)是否存在实数m,使
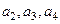 构成公差不为0的等差数列?若存在,请求出实数
构成公差不为0的等差数列?若存在,请求出实数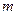 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;(III)求证:当
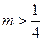 时,总能找到
时,总能找到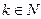 ,使得
,使得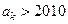 .
.
答案
(1)
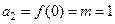 ,
,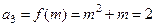 ,
,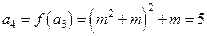 .
.(2)
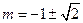
(3) 略
解析
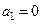 ,
,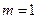 ,所以
,所以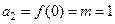 ,
,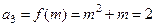 ,
,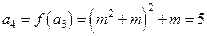 .…………4分
.…………4分(II)方法一:假设存在实数
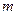 ,使得
,使得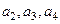 构成公差不为0的等差数列.
构成公差不为0的等差数列.由(I)得到
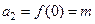 ,
,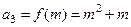 ,
,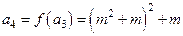 .因为
.因为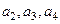 成等差数列,
成等差数列,所以
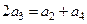 ,…………6分
,…………6分所以,
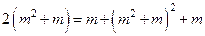 ,化简得
,化简得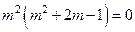 ,
,解得
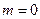 (舍),
(舍),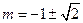 . …………8分
. …………8分经检验,此时
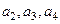 的公差不为0,
的公差不为0,所以存在
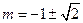 ,使
,使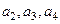 构成公差不为0的等差数列. …………9分
构成公差不为0的等差数列. …………9分方法二:因为
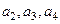 成等差数列,
成等差数列,所以
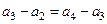 ,…………6分
,…………6分即
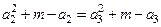 ,
,所以
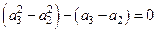 ,即
,即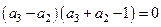 .
.因为
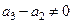 ,所以
,所以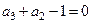 解得
解得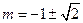 . …………8分
. …………8分经检验,此时
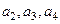 的公差不为0.
的公差不为0.所以存在
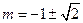 ,使
,使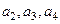 构成公差不为0的等差数列. …………9分
构成公差不为0的等差数列. …………9分(III)因为
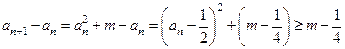 ,
,又
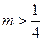 , 所以令
, 所以令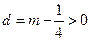 .
.由
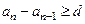 ,
,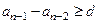 ,
,……
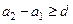 ,将上述不等式全部相加得
,将上述不等式全部相加得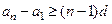 ,即
,即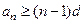 ,
,因此只需取正整数
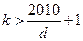 ,就有
,就有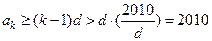 .………14分
.………14分
