题目
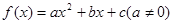 ,且
,且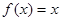 无实根,则下列命题中:
无实根,则下列命题中:(1)方程
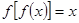 一定无实根;
一定无实根;(2)若
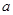 >0,则不等式
>0,则不等式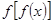 >
>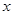 对一切实数
对一切实数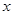 都成立;
都成立;(3)若
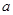 <0,则必存在实数
<0,则必存在实数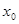 ,使得
,使得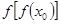 >
>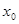 ;
;(4)若
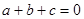 ,则不等式
,则不等式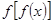 <
<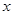 对一切
对一切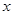 都成立。
都成立。其中正确命题的序号有 (写出所有真命题的序号)
答案
解析
分析:f[f(x)]为一个复合函数,可以把方括号里的f(x)看作为一个未知数t,t的范围就是f(x)的值域.由此入手进行判断,能够得到正确答案.
解答:解:f[f(x)]为一个复合函数,可以把方括号里的f(x)看作为一个未知数t,t的范围就是f(x)的值域.
(1):f[f(x)]可以看为f(t),而题中f(x)=x无实根,所以方程f[f(x)]=x无实根,故(1)成立;(2):和第一个一样的想法,依然把方括号里的f(x)看作为一个未知数t,则外层为一个开口向上的2次函数,
且f(x)=x无实根,所以a>0,则不等式f[f(x)]>x对一切实数x都成立,故(2)成立;(3):和2问同理,只不过a符号变了下,故(3)错误;(4):由条件得f(1)=0,把x=1代入里面得到了一个结论为c<1的结论,
这就说明若使(4)成立必有c<1,而满足大前提的c肯定是有可能取到小于1的数的,所以(4)对.
故答案为:(1)、(2)、(4).
