题目

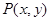已知是圆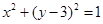上的动点，定点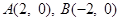，则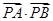
的最大值为    
                                           

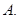
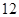
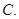
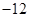
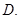
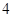
答案

A

解析

分析：由平面向量的数量积公式，可得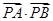的解析式；再由P（x，y）是圆x²+（y-3）²=1上的动点，可得x，y的取值范围；从而求得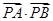的最大值（或最小值）．
解答：解：∵P（x，y）是圆x²+（y-3）²=1上的动点，且A（2，0），B（-2，0），
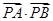∴=（2-x，0-y）?（-2-x，0-y）=（2-x）?（-2-x）+（-y）²=x²+y²-4，
由x²+（y-3）²=1，得x²+y²=6y-8，且2≤y≤4，∴x²+y²-4=6y-12≤24-12=12，
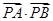∴的最大值为：12
故答案选：A．