题目

（本小题满分12分）已知二次函数f（x）=ax²+bx+c．
（1）若f（-1）=0，试判断函数f（x）零点的个数；
（2）是否存在a,b,c∈R，使f（x）同时满足以下条件：
①对任意x∈R,f（-1+x）=f（-1-x），且f（x）≥0;
②对任意x∈R,都有0≤f（x）-x≤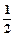（x-1）²．若存在，求出a,b,c的值；若不存在，请说
明理由。
（3）若对任意x₁、x₂∈R且x₁<x₂，f（x₁）≠f（x₂）,试证明：存在x₀∈（x₁,x₂）,使f（x₀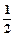）=[f（x₁）+f（x₂）]成立。

答案

解:（1）∵f（-1）=0,∴a-b+C=0,则b=a+c,∵⊿=b²-4ac=（a-c）²,∴当a=c时,⊿=0,
此函数f（x）有一个零点;当a≠c时,⊿>0．函数f（x）有两个零点．
（2）假设a,b,c存在,有（1）可知抛物线的对称轴为x=1,∴-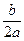=-1,即b=2a,①
由（2）可知对任意的x∈R,都有0≤f（x）-x≤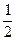（x-1）²,令x=1,
得0≤f（1）-1≤0,所以,f（1）=1,即a+b+c="1, " ②又因为f（x）-x≥0恒成立,
∴a>0
（b-1）²-4ac≤0 即（a-c）²≤0,∴a=c,③ 由①②③得a=C=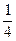,b=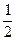
所以f（x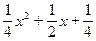）=,经检验a,b,c的值符合条件．
（3）令g（x）=f（x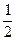）-[f（x₁）+f（x₂）],则
g（x₁）=f（x₁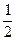）-[f（x₁）+f（x₂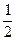）]=[f（x₁）-f（x₂）]  g（x₂）=f（x₂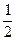）-[f（x₁）+f（x₂）]
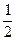={f（x₂）-f（x₁）},因为f（x₁）≠f（x₂）
所以,g（x₁）g（x₂）<0,所以g（x）=0在（x_1,x₂）内必有一个实根,
即存在x₀∈（x₁,x₂）使f（x₀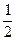）=[f（x₁）+f（x₂）]成立．

解析

略