题目
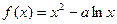 在
在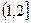 上是增函数,
上是增函数,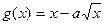 在
在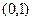 上为减函数。
上为减函数。(1)求f(x) ,g(x)的解析式;
(2)求证:当x>0时,方程f(
 x)=g(x)+2有唯一解。
x)=g(x)+2有唯一解。
答案
 解:(1)∵
解:(1)∵ f(x)=x
f(x)=x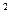 -alnx在(1,2]上是增函数,
-alnx在(1,2]上是增函数,∴f/(x)=2x-
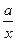 在(1,2]上大于等于零恒成立
在(1,2]上大于等于零恒成立∴a≤2x2
∴a≤2
又∵g(x)=x-
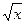 在(0,1)上为减函数。
在(0,1)上为减函数。∴g/(x)=1-
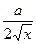 在(0,1)上小于等于零恒成立
在(0,1)上小于等于零恒成立∴a≥2
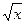
∴a≥2
∴a=2
∴f(x)=x
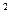 -2lnx, g(x)=x-2
-2lnx, g(x)=x-2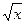
(2)设F(X)=" f(x)-" g(x)-2
∴F(X)= x
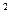 -2lnx-x+2
-2lnx-x+2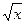 -2
-2∴F/(X)= 2X-
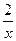 -1
-1 +
+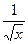 =
=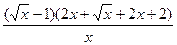
∵x>0
∴0<x<1时F/(X)〈0,F(X)单调递减,x>1时F/(X)>0 F(X)单调递增。
∴F(X)在x=1时取最小值
又∵F(1)=0
∴F(X)在x>0时有唯一解x=1
