题目
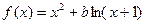 .
.(1)若
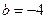 ,求函数
,求函数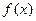 的单调区间;
的单调区间;(2)若函数
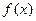 在定义域上是单调函数,求
在定义域上是单调函数,求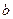 的取值范围;
的取值范围;(3)若
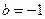 ,证明对任意
,证明对任意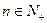 ,不等式
,不等式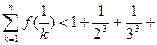 …
…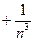 都成立。
都成立。
答案
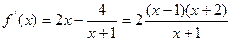 ,定义域
,定义域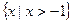
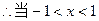 时,
时,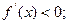 当
当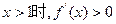 .
.故函数
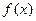 的减区间是(-1,1),增区间是(1,+
的减区间是(-1,1),增区间是(1,+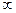 ).
).(2)∵
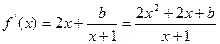 ,又函数
,又函数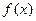 在定义域是单调函数,
在定义域是单调函数,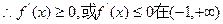 上恒成立。
上恒成立。若
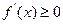 ,
,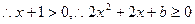 在
在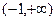 上恒成立,
上恒成立,即
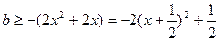 恒成立,由此得
恒成立,由此得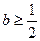 ;
;若
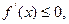 ∵
∵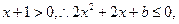 即
即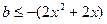 恒成立,
恒成立,因
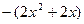 在
在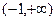 没有最小值,
没有最小值,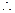 不存在实数
不存在实数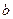 使
使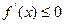 恒成立。
恒成立。综上所知,实数b的取值范围是
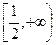 .
.(3)当
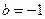 时,函数
时,函数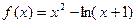 ,令函数
,令函数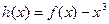
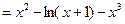 ,
,则
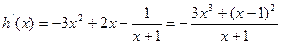 ,
,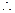 当
当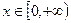 时,
时,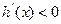 ,
,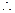 函数
函数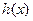 在
在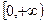 上单调递减,
上单调递减,又
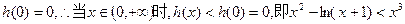 恒成立。
恒成立。故
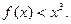 ∵
∵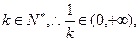 取
取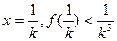 ,
, …
…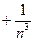 ,故结论成立。
,故结论成立。
