题目
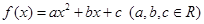 满足下列条件:
满足下列条件:①当
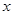 ∈R时,
∈R时,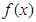 的最小值为0,且f (
的最小值为0,且f (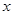 -1)=f(-
-1)=f(-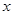 -1)成立;
-1)成立;②当
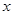 ∈(0,5)时,
∈(0,5)时,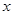 ≤
≤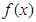 ≤2
≤2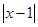 +1恒成立。
+1恒成立。(1)求
 的值;
的值; (2)求
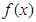 的解析式;
的解析式;(3)求最大的实数m(m>1),使得存在实数t,只要当
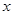 ∈
∈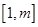 时,就有
时,就有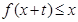 成立。
成立。
答案
(2)由①知二次函数的关于直线x=-1对称,且开口向上
故设此二次函数为f(x)=a(x+1)2,(a>0),∵f(1)=1,∴a=
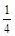
∴f(x)=
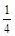 (x+1)2
(x+1)2(3)假设存在t∈R,只需x∈[1,m],就有f(x+t)≤x.
f(x+t)≤x
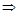
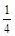 (x+t+1)2≤x
(x+t+1)2≤x x2+(2t-2)x+t2+2t+1≤0.
x2+(2t-2)x+t2+2t+1≤0.令g(x)=x2+(2t-2)x+t2+2t+1,g(x)≤0,x∈[1,m].
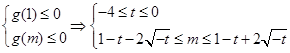
∴m≤1-t+2
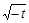 ≤1-(-4)+2
≤1-(-4)+2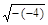 =9
=9t=-4时,对任意的x∈[1,9]
恒有g(x)≤0, ∴m的最大值为9.
