题目
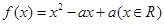 同时满足:①不等式
同时满足:①不等式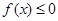 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在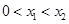 ,使得不等式
,使得不等式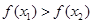 成立,设数列
成立,设数列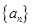 的前
的前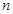 项和
项和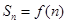 。
。(1)求函数
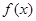 的表达式;
的表达式;(2)求数列
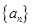 的通项公式;
的通项公式;(3)设各项均不为
 的数列
的数列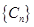 中,所有满足
中,所有满足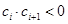 的整数
的整数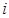 的个数称为这个数列
的个数称为这个数列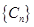 的变号数,令
的变号数,令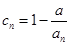 (
(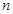
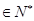 ),求数列
),求数列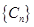 的变号数.
的变号数.
答案
(Ⅰ)∵不等式
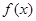 ≤0的解集有且只有一个元素 ∴
≤0的解集有且只有一个元素 ∴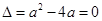 解得
解得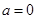 或
或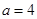
当
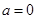 时,函数
时,函数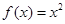 在
在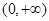 递增,不满足条件②
递增,不满足条件②当
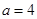 时,函数
时,函数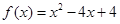 在(0,2)上递减,满足条件②
在(0,2)上递减,满足条件②综上得
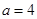 ,即
,即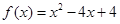
(Ⅱ)由(Ⅰ)知
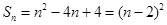 当
当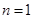 时,
时,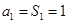
当
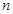 ≥2时
≥2时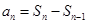 =
=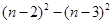 =
=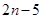 ∴
∴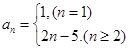
(Ⅲ)由题设可得
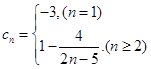 ∵
∵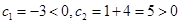 ,
,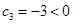 ,∴
,∴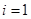 ,
,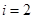 都满足
都满足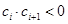 ∵当
∵当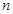 ≥3时,
≥3时,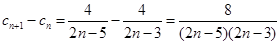
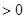
即当
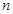 ≥3时,数列{
≥3时,数列{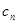 }递增,∵
}递增,∵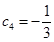
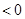 ,由
,由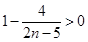
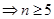 ,
,可知
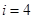 满足
满足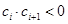 ∴数列{
∴数列{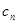 }的变号数为3.
}的变号数为3.
