题目
已知函数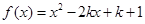 .
.
(Ⅰ)若函数在区间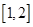 上有最小值
上有最小值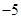 ,求
,求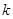 的值.
的值.
(Ⅱ)若同时满足下列条件①函数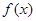 在区间
在区间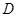 上单调;②存在区间
上单调;②存在区间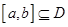 使得
使得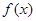 在
在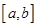 上的值域也为
上的值域也为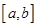 ;则称
;则称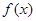 为区间
为区间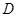 上的闭函数,试判断函数
上的闭函数,试判断函数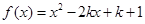 是否为区间
是否为区间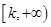 上的闭函数?若是求出实数
上的闭函数?若是求出实数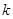 的取值范围,不是说明理由.
的取值范围,不是说明理由.
答案
(Ⅰ) 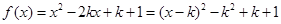 ,对称轴
,对称轴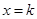
①当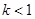 时,
时,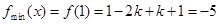 ,解得
,解得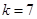 ,(舍去)
,(舍去)
②当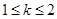 时,
时,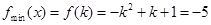 ,解得
,解得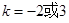 ,(舍去)
,(舍去)
③当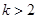 时,
时,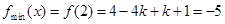 ,解得
,解得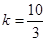 .
.
由①②③可得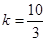 -----------------4分
-----------------4分
(Ⅱ)当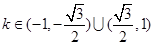 时,函数
时,函数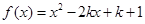 在
在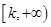 上是闭函数.-------6分
上是闭函数.-------6分
∵函数开口向上且对称轴为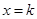 ,
,
∴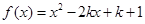 在
在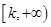 上单调递增.
上单调递增.
设存在区间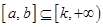 使得
使得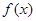 在
在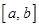 上的值域也为
上的值域也为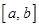
则有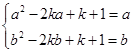 ,即方程
,即方程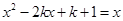 在
在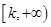 有两不同实数根 -8分
有两不同实数根 -8分
∴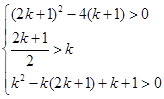 ,解得
,解得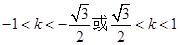
∴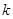 的取值范围为
的取值范围为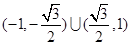
解析
略
