题目
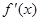 ,g¢(x),且
,g¢(x),且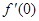 ="0,"
="0," 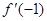 =−2,f(1)="g(1),"
=−2,f(1)="g(1)," 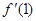 =g¢(1).
=g¢(1).(Ⅰ)求函数f(x),g(x)的解析式;
(Ⅱ)求F(x)=f(x)−g(x)的极小值;
(Ⅲ)是否存在实常数k和m,使得f(x)³kx+m和g(x)£kx+m成立?若存在,求出k和m的值;若不存在,说明理由.
答案
(Ⅰ)由已知得t=0,
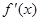 =2mx+n,
=2mx+n,则
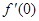 ="n=0,"
="n=0," 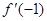 =−2m+n=−2,从而n="0," m=1,
=−2m+n=−2,从而n="0," m=1,∴f(x)=x2.
则
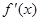 ="2x, " g¢(x)=3ax2+b.
="2x, " g¢(x)=3ax2+b.由f(1)="g(1),"
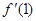 =g¢(1)得a+b−3=2,3a+b=2,解得a=−1,b=5,
=g¢(1)得a+b−3=2,3a+b=2,解得a=−1,b=5,∴g(x)=−x3+5x−3(x>0) ……4分
(Ⅱ)∵F(x)=f(x)−g(x)=x3+x2−5x+3(x>0),
求导数得F¢(x)=3x2+2x−5=(x−1)(3x+5)
∴F(x)在(0,1)单调递减,在(1,+¥)单调递增,从而F(x)的极小值为F(1)="0. " ……8分
(Ⅲ)因 f(x)与g(x)有一个公共点(1,1),而函数f(x)在点(1,1)的切线方程为y=2x−1.
下面验证
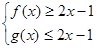 都成立即可.
都成立即可.由(x−1)2=x2−2x+1³0,得x2³2x−1,知f(x)³2x−1恒成立.
设h(x)=−x3+5x−3−(2x−1)= −x3+3x−2(x)>0,
求导数得h¢(x)=−3x2+3=−3(x+1)(x−1)(x>0),
∴h(x)在(0,1)上单调递增,在(1,+¥)上单调递减,所以h(x)=−x3+5x−3−(2x−1)的最大值为h(1)=0,
所以−x3+5x−3£2x−1,即g(x)£2x−1恒成立.
故存在这样的实常数k和m,且k=2,m=−1
