题目
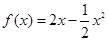 ,
,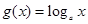 (
(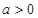 且
且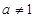 ).
).(1)过
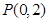 作曲线
作曲线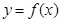 的切线,求切线方程;
的切线,求切线方程;(2)设
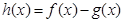 在定义域上为减函数,且其导函数
在定义域上为减函数,且其导函数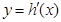 存在零点,求实数
存在零点,求实数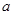 的值.
的值.
答案
设切点为Q(x0,y0),∵f′(x)=2-x,
∴k=f′(x0)=2-x0,且y0=f(x0)=2x0-
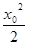 ,
,∴切线方程为y-2x0+
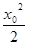 =(2-x0)(x-x0),即y=(2-x0)x+
=(2-x0)(x-x0),即y=(2-x0)x+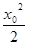 , ……3分
, ……3分∵(0,2)在切线上,代入可得x0=±2,……………………………5分
∴切线方程为y=2或y=4x+2. …………………………………7分
(2)h(x)=2x-
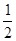 x2-logax在(0,+∞)上递减,
x2-logax在(0,+∞)上递减,∴h′(x)=2-x-
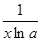 ≤0在(0,+∞)上恒成立,
≤0在(0,+∞)上恒成立,∵x>0,∴
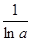 ≥2x-x2在(0,+∞)上恒成立.
≥2x-x2在(0,+∞)上恒成立.又2x-x2∈(-∞,1],∴
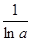 ≥1,∴0<lna≤1,①…………………10分
≥1,∴0<lna≤1,①…………………10分又∵h′(x)=2-x-
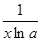 存在零点,
存在零点,即方程lna·x2-2lna·x+1=0有正根,
∴Δ=4ln2a-4lna≥0,∴lna≥1或lna<0,②…………………12分
由①②知lna=1,∴a=e.
