题目
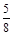 a-
a-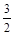 在闭区间
在闭区间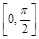 上的最大值是1?若存在,求出对应的a值;若不存在,说明理由.
上的最大值是1?若存在,求出对应的a值;若不存在,说明理由.
答案
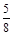 a-
a-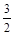 =
=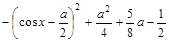
当0≤x≤
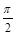 时,0≤cosx≤1,
时,0≤cosx≤1,若
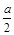 >1,即a>2,则当cosx=1时ymax=a+
>1,即a>2,则当cosx=1时ymax=a+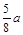 -
-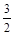 =1,∴a=
=1,∴a=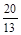 <2(舍去).
<2(舍去).若0≤
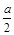 ≤1,即0≤a≤2,则当cosx=
≤1,即0≤a≤2,则当cosx=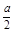 时,ymax=
时,ymax=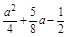 =1,∴a=
=1,∴a=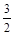 或a=-4(舍去).
或a=-4(舍去).若
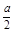 <0,即a<0时,则当cosx=0时,ymax=
<0,即a<0时,则当cosx=0时,ymax=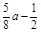 =1,∴a=
=1,∴a=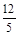 >0(舍去).
>0(舍去).综上所述,存在a=
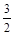 符合题设.
符合题设.
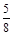 a-
a-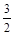 在闭区间
在闭区间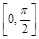 上的最大值是1?若存在,求出对应的a值;若不存在,说明理由.
上的最大值是1?若存在,求出对应的a值;若不存在,说明理由.
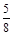 a-
a-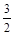 =
=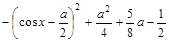
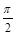 时,0≤cosx≤1,
时,0≤cosx≤1,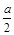 >1,即a>2,则当cosx=1时ymax=a+
>1,即a>2,则当cosx=1时ymax=a+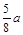 -
-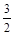 =1,∴a=
=1,∴a=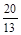 <2(舍去).
<2(舍去).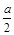 ≤1,即0≤a≤2,则当cosx=
≤1,即0≤a≤2,则当cosx=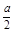 时,ymax=
时,ymax=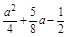 =1,∴a=
=1,∴a=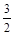 或a=-4(舍去).
或a=-4(舍去).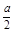 <0,即a<0时,则当cosx=0时,ymax=
<0,即a<0时,则当cosx=0时,ymax=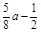 =1,∴a=
=1,∴a=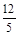 >0(舍去).
>0(舍去).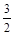 符合题设.
符合题设.