题目
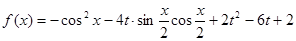
(
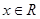 ),其中
),其中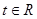 ,将
,将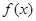 的最小值记为
的最小值记为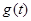 ,
,(1)求
 的表达式;
的表达式;(2)当
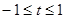 时,要使关于
时,要使关于 的方程
的方程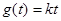 有且仅有一个实根,求实数
有且仅有一个实根,求实数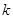 的取值范围.
的取值范围.
答案
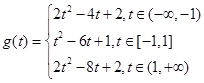 ;(2)
;(2)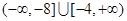 .
.
解析
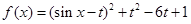 ,然后根据二次函数的性质讨论t的范围,进而确定
,然后根据二次函数的性质讨论t的范围,进而确定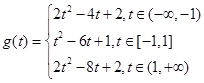 .
.(2) 当
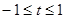 时,
时,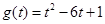 ,方程
,方程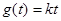 即:
即: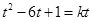 即方程
即方程 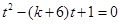 在区间
在区间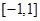 有且仅有一个实根.这是解决此问题的关键,下面转化为二次函数根的分布问题来解决即可.
有且仅有一个实根.这是解决此问题的关键,下面转化为二次函数根的分布问题来解决即可.解:(1)由已知有:
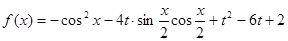
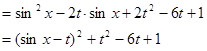
由于
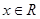 ,∴
,∴ 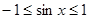 ………………………3分
………………………3分∴ 当
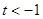 时,则当
时,则当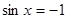 时,
时,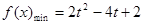 ;
;当
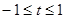 时,则当
时,则当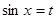 时,
时,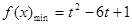 ;
;当
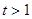 时,则当
时,则当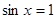 时,
时,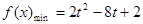 ;
;综上,
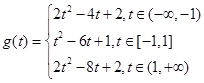 …………………7分
…………………7分(2)当
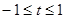 时,
时,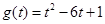 ,方程
,方程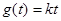 即:
即: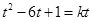 即方程
即方程 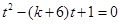 在区间
在区间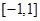 有且仅有一个实根,8分
有且仅有一个实根,8分令
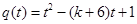 ,则有:
,则有:解法1:①若
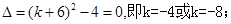
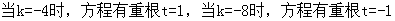
∴
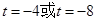 ……10分
……10分②
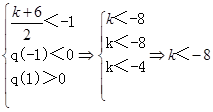 或
或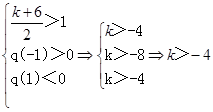
综上,当
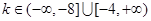 时,关于
时,关于 的方程
的方程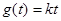 在区间
在区间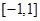 有且仅
有且仅有一个实根. ……………………………………14分
解法2:由
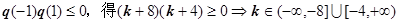 .
.
