题目
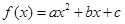 经过点
经过点
(1)求
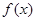 的解析式;
的解析式;(2)当
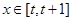 时,求
时,求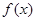 的最小值
的最小值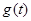 。
。
答案
当
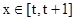 时利用定义域与对称轴的关系进行分类讨论得到结论。求解得到最小值。
时利用定义域与对称轴的关系进行分类讨论得到结论。求解得到最小值。
解析
(1)根据已知的点的坐标,设出二次函数的两根式,然后将第三个点代入得到参数a的值。
(2)在第一问的基础上可知,函数的开口和对称轴x=1,但是定义域与对称轴的关系不确定,因此分类讨论得到结论。
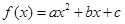 经过点
经过点
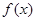 的解析式;
的解析式;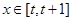 时,求
时,求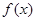 的最小值
的最小值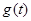 。
。
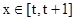 时利用定义域与对称轴的关系进行分类讨论得到结论。求解得到最小值。
时利用定义域与对称轴的关系进行分类讨论得到结论。求解得到最小值。