题目
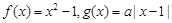 .
.(1)若关于
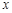 的方程
的方程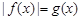 只有一个实数解,求实数
只有一个实数解,求实数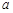 的取值范围;
的取值范围;(2)若当
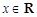 时,不等式
时,不等式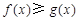 恒成立,求实数
恒成立,求实数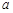 的取值范围。
的取值范围。
答案
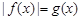 ,即
,即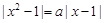 ,变形得
,变形得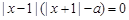 ,
,显然,
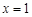 已是该方程的根,从而欲原方程只有一解,即要求方程
已是该方程的根,从而欲原方程只有一解,即要求方程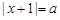 ,
,有且仅有一个等于1的解或无解,
结合图形得
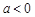 .……………………6分
.……………………6分(2)不等式
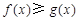 对
对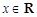 恒成立,即
恒成立,即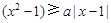 (*)对
(*)对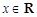 恒成立,
恒成立,①当
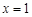 时,(*)显然成立,此时
时,(*)显然成立,此时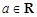 ; ……………………8分
; ……………………8分②当
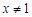 时,(*)可变形为
时,(*)可变形为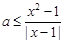 ,………………………10分
,………………………10分令
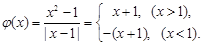 …………………………12
…………………………12因为当
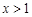 时,
时,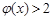 ,当
,当 时,
时,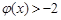 ,
,所以
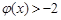 ,故此时
,故此时 . …………………15分
. …………………15分综合①②,得所求实数
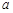 的取值范围是
的取值范围是 . …………………………………16分
. …………………………………16分
解析
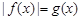 ,即
,即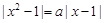 ,变形得
,变形得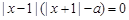 ,
,显然,
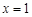 已是该方程的根,从而欲原方程只有一解,即要求方程
已是该方程的根,从而欲原方程只有一解,即要求方程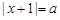 ,
,有且仅有一个等于1的解或无解,
结合图形得
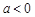 .
.第二问,不等式
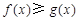 对
对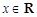 恒成立,即
恒成立,即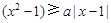 (*)对
(*)对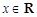 恒成立,
恒成立,①当
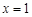 时,(*)显然成立,此时
时,(*)显然成立,此时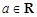 ;
; ②当
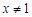 时,(*)可变形为
时,(*)可变形为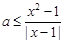
令
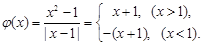
因为当
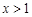 时,
时,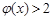 ,当
,当 时,
时,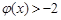 ,
,所以
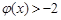 ,故此时
,故此时
