题目
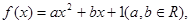 函数
函数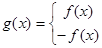
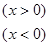
(1)若
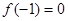 且函数
且函数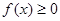 恒成立,求
恒成立,求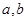 的值;
的值;(2)在(1)的条件下,当
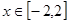 时,
时,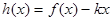 是单调函数,求
是单调函数,求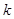 的取值范围.
的取值范围.(3)若
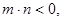
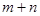 >0,
>0,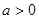 且
且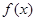 为偶函数,判断
为偶函数,判断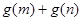 的符号(正或负)
的符号(正或负)并说明理由.
答案
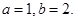 (2)
(2)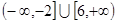 (3)
(3)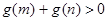
解析
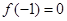 且函数
且函数 恒成立,可转化为
恒成立,可转化为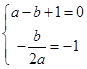 .解方程组即可.
.解方程组即可.(2)由题意可知
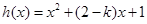 ,然后可利用二次函数的性质建立关于k的不等式求解.要注意此区间可能为增区间,也可能为减区间.
,然后可利用二次函数的性质建立关于k的不等式求解.要注意此区间可能为增区间,也可能为减区间.(3)首先根据f(x)为偶函数,可确定b=0,然后由
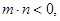
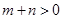 ,
,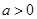 ,可得
,可得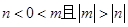 故
故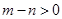 ,从而可得
,从而可得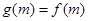 ,
, 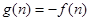
然后再研究g(m)+g(n)的符合即可.
解:(1)由已知
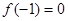 且函数
且函数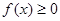 恒成立,
恒成立,所以
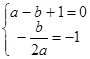 解得:
解得: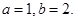 ………3分
………3分(2)由(1)
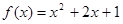 又
又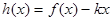
所以
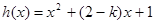
因为当
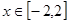 时,
时,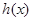 是单调函数
是单调函数所以
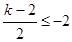 或
或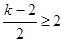 即
即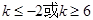
所以
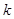 的取值范围是
的取值范围是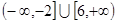 ………7分
………7分(3)因为
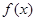 为偶函数,
为偶函数,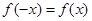
即
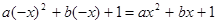

 所以
所以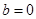
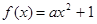
又
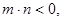
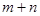 >0,
>0,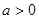
所以
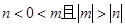 故
故 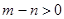
所以
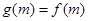
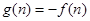

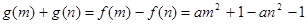
=

所以
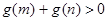 ………12分
………12分
