题目
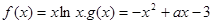
(1)求函数
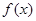 在
在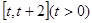 上的最小值;
上的最小值;(2)对一切
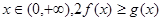 恒成立,求实数
恒成立,求实数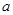 的取值范围.
的取值范围.
答案
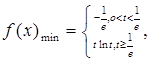 (2)a的范围是(-∞,4]。
(2)a的范围是(-∞,4]。
解析
(2)本小题实质是
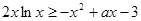 在
在 上恒成立,进一步转化为
上恒成立,进一步转化为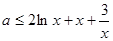 在
在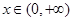 上恒成立,然后构造函数
上恒成立,然后构造函数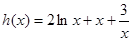 利用导数研究h(x)的最小值即可.
利用导数研究h(x)的最小值即可.(1)
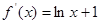 当
当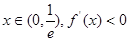
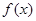 单调递减
单调递减 当
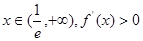
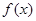 单调递增∵
单调递增∵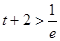
∴1°
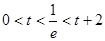 即
即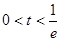 时
时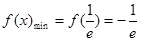
2°
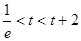 时
时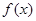 是递增的∴
是递增的∴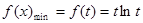
故
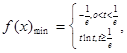
(2)
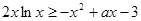 则
则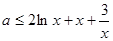 设
设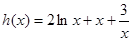
则
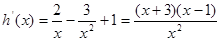
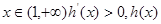 递增
递增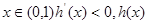 递减
递减 ∴
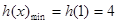 故所求a的范围是(-∞,4]
故所求a的范围是(-∞,4]
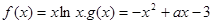
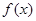 在
在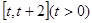 上的最小值;
上的最小值;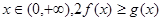 恒成立,求实数
恒成立,求实数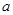 的取值范围.
的取值范围.
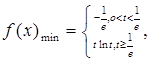 (2)a的范围是(-∞,4]。
(2)a的范围是(-∞,4]。
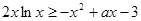 在
在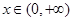 上恒成立,进一步转化为
上恒成立,进一步转化为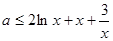 在
在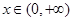 上恒成立,然后构造函数
上恒成立,然后构造函数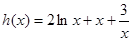 利用导数研究h(x)的最小值即可.
利用导数研究h(x)的最小值即可.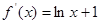 当
当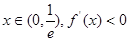
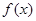 单调递减
单调递减 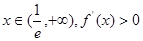
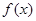 单调递增∵
单调递增∵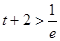
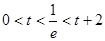 即
即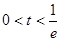 时
时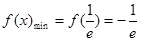
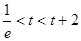 时
时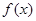 是递增的∴
是递增的∴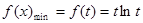
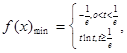
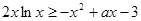 则
则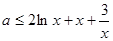 设
设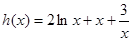
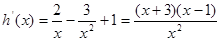
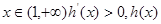 递增
递增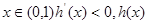 递减
递减 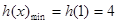 故所求a的范围是(-∞,4]
故所求a的范围是(-∞,4]