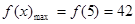题目
设
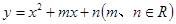 ,当
,当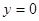 时,对应
时,对应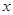 值的集合为
值的集合为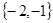 .
.(1)求
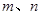 的值;(2)若
的值;(2)若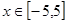 ,求该函数的最值.
,求该函数的最值.
答案
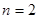 .(2)当
.(2)当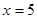 时,该函数取得最大值
时,该函数取得最大值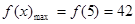
解析
(1)因为
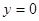 即
即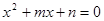 ,则
,则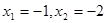 为其两根,
为其两根,由韦达定理知:
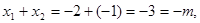 所以
所以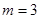 ,同理
,同理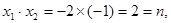 ,可知m,n的值。
,可知m,n的值。(2)因为由(1)知:
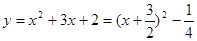 ,那个根据对称轴和定义域的关系而可知函数的最值。
,那个根据对称轴和定义域的关系而可知函数的最值。解:(1)
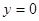 即
即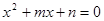 ,则
,则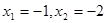 为其两根,
为其两根,由韦达定理知:
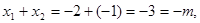 所以
所以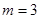 ,
, 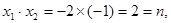 所以
所以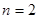 .
.(2)由(1)知:
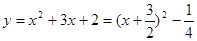 ,
,因为
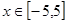 ,所以,当
,所以,当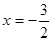 时,该函数取得最小值
时,该函数取得最小值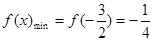 ,
,又因为
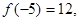
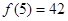 ,
,所以当
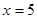 时,该函数取得最大值
时,该函数取得最大值