题目

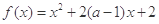函数在区间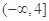上递减，则实数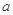的取值范围是（ ）

A．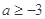

B．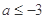

C．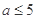

D．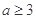

答案

B

解析

试题分析：本试题是二次函数中区间定轴动的问题，先求出函数的对称轴，再确定出区间与对称轴的位置关系求出实数a的取值范围。由题意，函数的对称轴是x=1-a
∵函数f（x）=x²+ax+3在区间（-∞，2]上递减,则只要满足区间在对称轴的的左侧即可，那么必有， 1-a≥4，解得a≤-3,故答案为：a≤-3,选B.
点评：解答本题的关键是熟练掌握了二次函数的性质与图象，根据其性质与图象直接得出关于参数的不等式，求出其范围